El
Colegio Gil de Jaz, el Ayuntamiento, el Palacio de Sada, la Portada de San
Esteban, sus ábsides y otros muchos edificios y construcciones de Sos del Rey Católico nos
parecen ya bellos a simple vista, sin entrar a profundizar en técnicas arquitectónicas
o elementos artísticos, decorativos o constructivos. Y esta belleza natural que vemos, y de la que disfrutamos en estos
monumentos, responde sencillamente a la total armonía de sus formas.
Para que algo sea bello tiene que estar completo, íntegro; lo inacabado es, por principio, feo; lo bello ha de ser nítido, claro, y ha de presentar una proporción adecuada, una armonía. La belleza de las construcciones antes mencionadas responden a una armonía que no es casual, sino al hecho de que su construcción está integrada en la "sección áurea" o "divina proporción", también llamada proporción áurea, el número aúreo, el número de oro, proporción dorada, la estética de las proporciones, el número “fi” (phi), la sucesión de Fibonacci...
Para que algo sea bello tiene que estar completo, íntegro; lo inacabado es, por principio, feo; lo bello ha de ser nítido, claro, y ha de presentar una proporción adecuada, una armonía. La belleza de las construcciones antes mencionadas responden a una armonía que no es casual, sino al hecho de que su construcción está integrada en la "sección áurea" o "divina proporción", también llamada proporción áurea, el número aúreo, el número de oro, proporción dorada, la estética de las proporciones, el número “fi” (phi), la sucesión de Fibonacci...
Aunque a principios del siglo XVI se le llamó “Divina
Proporción”, ya se conoce su existencia en los
pentagramas de las tabletas sumerias del 3.299 a. de C. Usada también en la
antigua Grecia, se utilizó para establecer las proporciones de los templos
y en las composiciones de las
esculturas, empleándose también mucho en la arquitectura y otras artes
plásticas del Renacimiento.
Santo Tomás decía: " Llamamos bello al hombre cuando sus miembros guardan las proporciones adecuadas en sus dimensiones y disposición, y cuando su color es claro y nítido". Y sobre arquitectura: ”(…) en un bello edificio las dimensiones de cada parte están determinadas en función de relaciones de las otras partes ” y, haciendo un símil con la música, continúa: “…y todas (las partes) son musicalmente solidarias de la forma del conjunto(…)”[1], es decir, todas las partes tenían que estar en armonía entre sí y éstas con su globalidad.
El conocimiento básico de la proporción empleado por los artistas occidentales ya se tenía 300 años a. de C. cuando Euclides resumió el conocimiento matemático del mundo antiguo en el libro llamado los Elementos, estableciendo los principios que sustentan la ciencia de la geometría. En la parte de los Elementos dedicada a las proporciones, Euclides demostraba que el fundamento de un sistema de proporciones es una razón, siendo y expresando dicha razón una comparación cuantitativa entre dos cosas. La razón más importante que se demuestra en los Elementos, a la que Platón llamó “la sección”, ha sido empleada constantemente desde entonces por los artistas. Posteriormente, en el siglo XIX, se la conoció como “sección áurea”, empleando con frecuencia los artistas el rectángulo de sección áurea porque de él se deriva un atractivo conjunto de formas cuyas áreas se miden con ellas mismas y con la forma modelo, facilitando la relación proporcional básica de las partes con el todo. Esta relación puede medirse y, con la práctica, percibirse a simple vista. La constancia de la relación y la divisibilidad armónica son las cualidades fundamentales de la proporción y son las causas de la atracción que ejercen en los artistas y lo que hace que algo que contenga esta “divina proporción” nos parezca bello a simple vista.
Santo Tomás decía: " Llamamos bello al hombre cuando sus miembros guardan las proporciones adecuadas en sus dimensiones y disposición, y cuando su color es claro y nítido". Y sobre arquitectura: ”(…) en un bello edificio las dimensiones de cada parte están determinadas en función de relaciones de las otras partes ” y, haciendo un símil con la música, continúa: “…y todas (las partes) son musicalmente solidarias de la forma del conjunto(…)”[1], es decir, todas las partes tenían que estar en armonía entre sí y éstas con su globalidad.
El conocimiento básico de la proporción empleado por los artistas occidentales ya se tenía 300 años a. de C. cuando Euclides resumió el conocimiento matemático del mundo antiguo en el libro llamado los Elementos, estableciendo los principios que sustentan la ciencia de la geometría. En la parte de los Elementos dedicada a las proporciones, Euclides demostraba que el fundamento de un sistema de proporciones es una razón, siendo y expresando dicha razón una comparación cuantitativa entre dos cosas. La razón más importante que se demuestra en los Elementos, a la que Platón llamó “la sección”, ha sido empleada constantemente desde entonces por los artistas. Posteriormente, en el siglo XIX, se la conoció como “sección áurea”, empleando con frecuencia los artistas el rectángulo de sección áurea porque de él se deriva un atractivo conjunto de formas cuyas áreas se miden con ellas mismas y con la forma modelo, facilitando la relación proporcional básica de las partes con el todo. Esta relación puede medirse y, con la práctica, percibirse a simple vista. La constancia de la relación y la divisibilidad armónica son las cualidades fundamentales de la proporción y son las causas de la atracción que ejercen en los artistas y lo que hace que algo que contenga esta “divina proporción” nos parezca bello a simple vista.
Este dominio de la geometría y aritmética fue aprendido por los maestros constructores de la Edad Media a través de Vitrubio, de cuyo manuscrito De Architectura se hallaban versiones en las bibliotecas de algunos monasterios románicos.
La belleza vitrubiana se basaba en la proportio, dimensión principal que ordena y relaciona los componentes secundarios de una obra, y en la symmetria, es decir, en un módulo que se multiplica para obtener una composición general, principios que se concretan, entre otros presupuestos, en la cuadriculación y triangulación de las formas, así como en la perfección de la escuadra.
La belleza vitrubiana se basaba en la proportio, dimensión principal que ordena y relaciona los componentes secundarios de una obra, y en la symmetria, es decir, en un módulo que se multiplica para obtener una composición general, principios que se concretan, entre otros presupuestos, en la cuadriculación y triangulación de las formas, así como en la perfección de la escuadra.
Es decir, una sección áurea es una división
en dos de un segmento según proporciones dadas por el número áureo. Este número
áureo o número de oro se simboliza con la letra griega φ (ϕ) (phi)
y su valor numérico es 1,6180339887…., uno de los mayores
tesoros de la geometría: la medida de oro.
Veamos un dibujo de un rectángulo de
sección áurea para entenderlo mejor.
La
línea E-F muestra la división de las dos proporciones principales y cómo el
rectángulo ABCD de sección áurea siempre contiene un cuadrado (EFDC) y un rectángulo
(BAFE) también de sección áurea. Este rectángulo BAFE contiene otro rectángulo de sección áurea menor(BGHE)
más otro cuadrado(GAFH), y así sucesivamente, guardando siempre la misma
proporción.
La espiral del dibujo muestra cómo estas formas y las relaciones
entre ellas se repiten a sí mismas. La repetición geométrica, o
progresión, toma la forma de una razón proporcional, donde cada cantidad
permanece en la misma relación con su predecesora, del mismo modo que lo hace
su sucesora. De aquí que la relación sea constante en toda la secuencia de
magnitudes crecientes.
Esta constante relación nos permite
trazar una espiral, la más bella curva matemática, cuya forma se mantiene
constante, pudiendo extenderse indefinidamente hacia dentro o hacia afuera,
pero siempre de forma homotética, o sea, semejante a sí misma, exactamente
igual que el principio biológico del ritmo creciente de las conchas de algunos
moluscos y cuernos de animales, que crecen a lo largo y ancho del animal para
adaptarse al crecimiento del mismo, pero permaneciendo siempre homotéticos. Esta espiral se conoce con el nombre de espiral logarítmica, equiangular, espiral áurea o espiral de Durero, quien en su "Instrucción sobre la medida con regla y compás de figuras planas y sólidas", publicado en 1525, describía cómo trazar con estos instrumentos la espiral áurea, basada en la sección áurea.
ϕ (phi),
el número áureo, deriva de una sucesión de números que descubrió el matemático
pisano Leonardo Bigollo, más conocido como Fibonacci, y que vivió entre los
siglos XII y XIII. Se trata de una sucesión infinita de números naturales que
comienza con los números 1 y 1 y, a partir de aquí, el siguiente se obtiene
sumando los dos anteriores: 1,1,2,3,5,8,13,21,34,55,89,144,233,…Si dividimos
cualquier número de esta sucesión entre el que le precede obtenemos una cifra
muy similar al número áureo (1.61803…). Aplicando este concepto aritmético a la
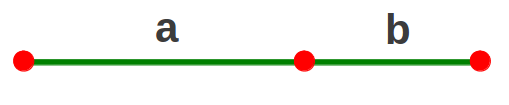
sección áurea y dividimos, como antes hemos señalado, el total de la longitud
del segmento A+B entre la parte más larga A, obtenemos el mismo resultado que
al dividir la parte más larga A entre la más corta B, cuyo resultado es
1.6180339887… , o sea, el número ϕ o número
áureo.
Veámoslo más claramente con un
ejemplo gráfico:
| El siguiente número en la sucesión de Fibonacci sería el 55 (a+b = 34+21). 34 ➗ 21 = 1.61. a+b (55) ➗ a (34) = 1.61. |
En Sos del Rey Católico, como se ha
indicado al principio de este post, existen numerosos ejemplos de belleza debido a las proporciones
áureas en muchos edificios de la villa, ya sean de la Edad Media, Moderna o
Contemporánea, pues tanto los maestros constructores de antaño como los arquitectos más contemporáneos conocían y conocen la belleza de la sección áurea y no dudaron en aplicarla a sus obras y construcciones.
¿Por qué los majestuosos ábsides de la iglesia de San Esteban, en Sos del Rey Católico, además de colosales nos parecen tan bellos? Sencillamente porque sus formas están en proporción y armonía y los diferentes tramos absidales están construidos guardando la Divina Proporción conteniendo, entre los distintos elementos que los componen, el número de oro. El maestro constructor, un verdadero artista, supo dimensionar perfectamente los ábsides en altura con proporciones áureas.
Observemos, por ejemplo, los tramos superiores de los ábsides, donde se abren las ventanas. Vemos que estos están limitados y enmarcados en la base por la imposta inferior de ajedrezado jaqúes de las dos que adornan los tambores, justo en el arranque de las ventanas; a los lados, por los contrafuertes que, desde el suelo, recorren en altura los ábsides (por sendos contrafuertes si observamos la parte central del ábside central o por uno de ellos y el acoplamiento del ábside lateral si observamos cualquiera de las dos zonas laterales); y completando la enmarcación, en la parte superior, por la cornisa o tejaroz de los mismos.
Vamos a fijarnos en la zona central del ábside mayor de la iglesia. Esta "enmarcación" constituye exactamente un rectángulo de sección áurea, donde la línea que pasa por el punto de arranque de las arquivoltas que conforman las ventanas, coincidiendo con la imposta superior, sería la "sección", "mediana" o "corte" del rectángulo áureo. Si dividimos la altura desde la imposta inferior al tejaroz entre la distancia desde la imposta superior al tejaroz obtendremos el número de oro. Los ábsides laterales, más pequeños que el central, con ventanas más pequeñas y tambores más reducidos, guardan la debida proporción y también están inmersos en rectángulos aúreos.
Como la fotografía que vemos al margen está tomada desde la base de los ábsides, con el objetivo de la cámara orientado hacia arriba, la propia perspectiva nos falsea la realidad y nos hace imposible poder señalarlo y dibujarlo gráficamente sobre la imagen de la foto, por lo que añadimos un dibujo planimétrico de proyección horizontal para su mejor comprensión.
Además, éste rectángulo áureo está incluido en otro inferior, también áureo, desde la imposta superior hasta la separación de la iglesia inferior con la superior donde, a mitad de altura de los ábsides, los radios absidales decrecen un poco al mismo nivel en que los contrafuertes que se alzan desde el suelo se estrechan en grosor (ver dibujo). Si dividimos la altura desde la separación de las iglesias baja y alta hasta la imposta superior entre la distancia desde la misma hasta la imposta inferior, volvemos a obtener el número phi. Es decir, que las dos impostas de ajedrezado jaqués son las secciones áureas de sendos rectángulos áureos.
Pero no queda ahí la cosa: la altura de la ventana resulta ser la sección áurea de otro rectángulo áureo que resulta de la intersección de los dos anteriores. ¿ Cómo no van a ser bellos los ábsides de la iglesia de San Esteban con esta perfecta armonía y proporción geométrica?
Pero no sólo los ábsides son bellos por guardar la Divina Proporción. Ya hemos dicho que cada parte del edificio, además de guardar relación de proporcionalidad entre ellas, también la han de tener en el conjunto global de la obra. Otros ejemplos que guardan perfectamente la proporción áurea es la portada románica del templo, tanto en la portada original como en el atrio que se le añadió en el siglo XVI. Igualmente sucede con las bóvedas, ventanas, capillas y otros elementos del interior del templo; el túnel de Santa Mª del Perdón...Todas las partes guardan la Divina Proporción, por lo que toda la iglesia, en conjunto, es una belleza, puesto que sus artífices tenían que construir "el templo de Dios". Como decía Plotino: "...es la proporción de unas partes con otras y con el conjunto [...] la que constituye la belleza visible, y que para las cosas visibles, como para todas las demás en general, el ser bellas consiste en estar bien proporcionadas y medidas. [...] Si el conjunto es bello, también las partes deben ser bellas, pues cierto es que la belleza no debe constar de partes feas, sino que debe haber tomado posesión de todas ellas"[3]
También, en otras construcciones posteriores en el tiempo, como el Colegio Gil de Jaz o Ayuntamiento, apreciamos la belleza de la fachada debido a sus "Divinas Proporciones". Asímismo, otros muchos edificios, monumentos y casas de Sos del Rey Católico guardan también la proporción áurea: Palacio Español de Niño, Palacio de Sada, Lonja, casa Mesejuán, casa Fuertes..., sólo es cuestión de saberla descubrir “a simple vista”, que, aunque las primeras veces puede resultar algo enredoso y dificultoso, con la práctica, observando detenidamente los edificios, resulta más sencillo de lo que parece. Os animo a que lo descubráis.
Túnel del Perdón, Palacio de Sada o casa Mesejuán, entre otros muchos edificios en la villa de Sos del Rey Católico, guardan la Divina Proporción en su construcción.
En resumen, la belleza que los arquitectos románicos alcanzaron en sus obras fue fruto de la armonía de la composición, de la grandeza de las dimensiones y de la pulcritud del trabajo de la materia. Este es el secreto de la belleza que, además de aparecer espontáneamente en la naturaleza (moluscos, flores, árboles...), muchos artistas han usado en sus obras y creaciones a lo largo de la historia y que actualmente se sigue utilizando y aplicando en muchos otros campos, como en música, informática, márketing, fotografía, electrónica, artículos de consumo, juegos... Por ejemplo, el iPod classic de Apple, el D.N.I, las cajetilla de tabaco o las tarjetas de crédito, basan sus medidas en un rectángulo áureo.
___________________________
[1] Santo Tomás. Expositio super Dionysium De divinis nominibus, 362. Cfr. Mª José López Terrada. Introducción a la historia de las ideas estéticas: La Edad Media, p. 163.
[2]Ginés de Albareda. “Sos del Rey Católico”. Cuadernos de Aragón, 7, p.126.
[3] Plotino. Enéada. Tratado I, 6; p. 276. Edición de Jesús Gial.
BIBLIOGRAFÍA
Ginés
de Alvareda, escritor y profesor de literatura hispanoamericana, ya comentaba
la belleza de los ábsides de Sos al describir la precisión y equilibrio de sus
elementos : “…Puede ser que la más
perfecta solución arquitectónica sea el ábside románico, y estos tres de la
iglesia de Sos tienen la precisión de contorno y equilibrio que se siente la
piedra como transfigurada. Los arcos son airosos y encumbrados; las columnas
esbeltas, con criterio ascendente, y justa la anchura de la luz. Es joya,
auténtica joya, esta iglesia románica de Sos…”[2]. Alvareda estaba
observando, implícitamente, las “divinas proporciones” de los ábsides.
Los maestros arquitectos del románico levantaban las iglesias para construir “la casa de Dios” en la tierra, por eso sus construcciones trataban de ser lo más bellas y perfectas posibles. Pero para ello tenían que edificar con conocimientos de tipo proporcional y geométrico que le facilitaran el trabajo. Conocimientos que, como antes hemos indicado, los artífices del Medioevo ya conocían de antemano, además de venir siendo utilizados desde hace siglos, y la iglesia de San Esteban no iba a ser una excepción.
Los maestros arquitectos del románico levantaban las iglesias para construir “la casa de Dios” en la tierra, por eso sus construcciones trataban de ser lo más bellas y perfectas posibles. Pero para ello tenían que edificar con conocimientos de tipo proporcional y geométrico que le facilitaran el trabajo. Conocimientos que, como antes hemos indicado, los artífices del Medioevo ya conocían de antemano, además de venir siendo utilizados desde hace siglos, y la iglesia de San Esteban no iba a ser una excepción.
 |
| Abside central. Iglesia de San Esteban. Sos del Rey Católico |
Vamos a fijarnos en la zona central del ábside mayor de la iglesia. Esta "enmarcación" constituye exactamente un rectángulo de sección áurea, donde la línea que pasa por el punto de arranque de las arquivoltas que conforman las ventanas, coincidiendo con la imposta superior, sería la "sección", "mediana" o "corte" del rectángulo áureo. Si dividimos la altura desde la imposta inferior al tejaroz entre la distancia desde la imposta superior al tejaroz obtendremos el número de oro. Los ábsides laterales, más pequeños que el central, con ventanas más pequeñas y tambores más reducidos, guardan la debida proporción y también están inmersos en rectángulos aúreos.
Como la fotografía que vemos al margen está tomada desde la base de los ábsides, con el objetivo de la cámara orientado hacia arriba, la propia perspectiva nos falsea la realidad y nos hace imposible poder señalarlo y dibujarlo gráficamente sobre la imagen de la foto, por lo que añadimos un dibujo planimétrico de proyección horizontal para su mejor comprensión.
 |
| Zona central del ábside mayor o central de la iglesia de San Esteban. Sos del Rey Católico |
Además, éste rectángulo áureo está incluido en otro inferior, también áureo, desde la imposta superior hasta la separación de la iglesia inferior con la superior donde, a mitad de altura de los ábsides, los radios absidales decrecen un poco al mismo nivel en que los contrafuertes que se alzan desde el suelo se estrechan en grosor (ver dibujo). Si dividimos la altura desde la separación de las iglesias baja y alta hasta la imposta superior entre la distancia desde la misma hasta la imposta inferior, volvemos a obtener el número phi. Es decir, que las dos impostas de ajedrezado jaqués son las secciones áureas de sendos rectángulos áureos.
Pero no queda ahí la cosa: la altura de la ventana resulta ser la sección áurea de otro rectángulo áureo que resulta de la intersección de los dos anteriores. ¿ Cómo no van a ser bellos los ábsides de la iglesia de San Esteban con esta perfecta armonía y proporción geométrica?
 |
| La portada de San Esteban está encuadrada en un perfecto rectángulo áureo |
Pero no sólo los ábsides son bellos por guardar la Divina Proporción. Ya hemos dicho que cada parte del edificio, además de guardar relación de proporcionalidad entre ellas, también la han de tener en el conjunto global de la obra. Otros ejemplos que guardan perfectamente la proporción áurea es la portada románica del templo, tanto en la portada original como en el atrio que se le añadió en el siglo XVI. Igualmente sucede con las bóvedas, ventanas, capillas y otros elementos del interior del templo; el túnel de Santa Mª del Perdón...Todas las partes guardan la Divina Proporción, por lo que toda la iglesia, en conjunto, es una belleza, puesto que sus artífices tenían que construir "el templo de Dios". Como decía Plotino: "...es la proporción de unas partes con otras y con el conjunto [...] la que constituye la belleza visible, y que para las cosas visibles, como para todas las demás en general, el ser bellas consiste en estar bien proporcionadas y medidas. [...] Si el conjunto es bello, también las partes deben ser bellas, pues cierto es que la belleza no debe constar de partes feas, sino que debe haber tomado posesión de todas ellas"[3]
 |
| Túnel de Santa María del Perdón |
 |
| Palacio de los Sada |
Túnel del Perdón, Palacio de Sada o casa Mesejuán, entre otros muchos edificios en la villa de Sos del Rey Católico, guardan la Divina Proporción en su construcción.
En resumen, la belleza que los arquitectos románicos alcanzaron en sus obras fue fruto de la armonía de la composición, de la grandeza de las dimensiones y de la pulcritud del trabajo de la materia. Este es el secreto de la belleza que, además de aparecer espontáneamente en la naturaleza (moluscos, flores, árboles...), muchos artistas han usado en sus obras y creaciones a lo largo de la historia y que actualmente se sigue utilizando y aplicando en muchos otros campos, como en música, informática, márketing, fotografía, electrónica, artículos de consumo, juegos... Por ejemplo, el iPod classic de Apple, el D.N.I, las cajetilla de tabaco o las tarjetas de crédito, basan sus medidas en un rectángulo áureo.
___________________________
[1] Santo Tomás. Expositio super Dionysium De divinis nominibus, 362. Cfr. Mª José López Terrada. Introducción a la historia de las ideas estéticas: La Edad Media, p. 163.
[2]Ginés de Albareda. “Sos del Rey Católico”. Cuadernos de Aragón, 7, p.126.
[3] Plotino. Enéada. Tratado I, 6; p. 276. Edición de Jesús Gial.
BIBLIOGRAFÍA
-BENEDICTO SALAS, ROBERTO. La construcción de la arquitectura románica. I.F.C. Colección Estudios: Arte. Zaragoza, 2015.
-BONEL, CARMEN. La divina proporción. Las formas geométricas. 2ª edición. Ediciones UPC. Barcelona, 2000.
-BONEL, CARMEN. La divina proporción. Las formas geométricas. 2ª edición. Ediciones UPC. Barcelona, 2000.
-DOMINGUEZ MURO, MARIANO J. El número de oro. Ed. Proyecto Sur.
Granada, 1999.
-FRAYLING, CHRISTOPHER; FRAYLING, HELEN; VAN DER MEER, RON. Carpeta de Arte. Un recorrido único y tridimensional por la creación
del arte. Ed. Destino.
-GINÉS DE ALVAREDA. "Sos del Rey Católico", Cuadernos de Aragón, 7, pp. 123-129, I.F.C. Zaragoza, 1975.
-LÓPEZ TERRADA, Mª JOSÉ. Introducción a la historia de las ideas estéticas: La Edad Media. Universidad de Valencia, 2011.
-PLOTINO. Enéadas, I-II. Edición de Jesús Igal. Ed. Gredos. Madrid, 1982.
-ULRICH VON STRASSBURG. De summo bono. Ed. Meiner Félix Verlag. Hamburg (Alemania), 2011.
-Historia del Arte Español. Tomo IV; La época de los monasterios. La plenitud del románico. Dir: Joan Sureda. Planeta, 1995.
-Historia del Arte Español. TomoV; La época de las catedrales. El esplendor del gótico. Dir: Joan Sureda. Planeta, 1995.
-GINÉS DE ALVAREDA. "Sos del Rey Católico", Cuadernos de Aragón, 7, pp. 123-129, I.F.C. Zaragoza, 1975.
-LÓPEZ TERRADA, Mª JOSÉ. Introducción a la historia de las ideas estéticas: La Edad Media. Universidad de Valencia, 2011.
-PLOTINO. Enéadas, I-II. Edición de Jesús Igal. Ed. Gredos. Madrid, 1982.
-ULRICH VON STRASSBURG. De summo bono. Ed. Meiner Félix Verlag. Hamburg (Alemania), 2011.
-Historia del Arte Español. Tomo IV; La época de los monasterios. La plenitud del románico. Dir: Joan Sureda. Planeta, 1995.
-Historia del Arte Español. TomoV; La época de las catedrales. El esplendor del gótico. Dir: Joan Sureda. Planeta, 1995.
En la web:
-www.iboenweb.com. Fi (ϕ) La divina proporción o sección áurea.
-www.ovacen.com. Proporción áurea: Qué es y
cómo encontrarla.




No hay comentarios:
Publicar un comentario